HILL CLIMBING ALGORITHM IN AI

Introduction

Hill Climbing is an important local search algorithm used in Artificial Intelligence (AI) to solve optimization problems. Unlike traditional graph search algorithms such as BFS and DFS, hill climbing does not try to explore the entire search space. Instead, it focuses on improving a single solution step by step until no better solution is found.

Hill climbing is inspired by a real-life hill climbing scenario, where a person tries to reach the top of a hill by continuously moving upward. The person does not know the full landscape of the hill and can only see nearby locations. Similarly, the hill climbing algorithm makes decisions based only on local information.

Definition

Hill Climbing is a heuristic-based local search algorithm that starts from an initial state and repeatedly moves to a neighboring state that has a better heuristic value, until no better neighboring state exists.

In simple words:

Hill climbing always chooses the next best local option.

Key Characteristics of Hill Climbing

• It is a local search algorithm
• Uses a heuristic (evaluation) function
• Works by incremental improvement
• Does not store the search tree
• Stops when no improvement is possible

Basic Idea of Hill Climbing

The basic idea can be explained using a real-life analogy:

Imagine you are standing somewhere on a hill:

• You want to reach the highest point
• You can only see the nearby area
• You move in the direction that goes upward
• You stop when all nearby directions go downward

Similarly, hill climbing:

• Starts with a random or given initial solution
• Looks at neighboring solutions
• Moves to the neighbor with better value
• Stops when no neighbor is better

Important Terminology

• State: A possible solution
• Initial State: Starting solution
• Neighbor State: A solution obtained by a small change
• Heuristic Function (h): Measures how good a state is
• Goal State: Best or near-best solution
• Local Maximum: A peak that is not the global best
• Global Maximum: The best possible solution

Working of Hill Climbing Algorithm (Step by Step)

1. Select an initial state randomly or by some rule
2. Evaluate the initial state using a heuristic function
3. Generate all neighboring states
4. Compare the heuristic value of neighbors with the current state
5. Move to the neighbor with the highest improvement
6. Set this neighbor as the new current state
7. Repeat steps 3–6
8. Stop when no neighbor has a better heuristic value

At this point, the algorithm terminates.

Graphical Explanation of Hill Climbing

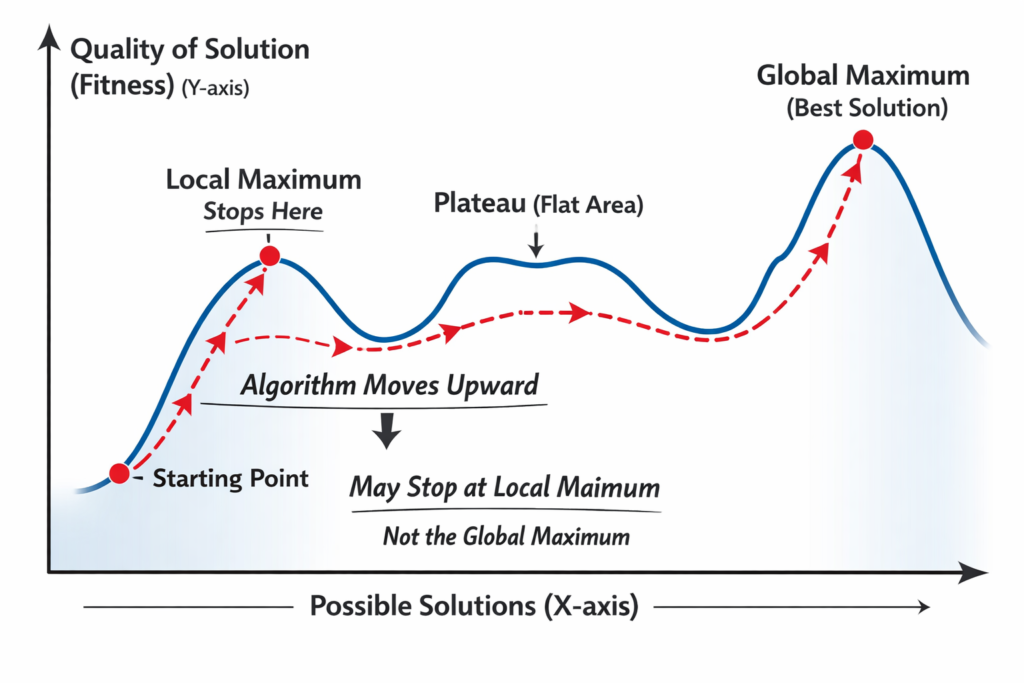
Explanation of Diagram

• X-axis → possible solutions
• Y-axis → quality of solution (fitness)
• The algorithm moves upward
• It may stop at a local maximum, not the global maximum

Types of Hill Climbing Algorithms

1. Simple Hill Climbing

• Evaluates neighbors one by one
• Moves to the first better neighbor
• Faster but less accurate
• May miss better solutions

2. Steepest-Ascent Hill Climbing

• Evaluates all neighbors
• Chooses the best possible neighbor
• More accurate
• Slower than simple hill climbing

3. Stochastic Hill Climbing

• Randomly selects one of the better neighbors
• Reduces chance of getting stuck
• Useful for large and complex search spaces

Problems Faced by Hill Climbing

1. Local Maximum

A state that is better than its neighbors but not the best overall solution.

➡ Algorithm stops prematurely.

2. Plateau

A flat region where neighboring states have the same value.

➡ Algorithm cannot decide which direction to move.

3. Ridge

A narrow region where improvement is possible but not directly reachable.

➡ Algorithm oscillates or moves slowly.

Why Hill Climbing Fails Sometimes

• Uses only local information
• Cannot look ahead
• No backtracking
• Strongly depends on the initial state

Advantages of Hill Climbing

1. Simple and easy to implement
2. Requires very little memory
3. Fast execution
4. Suitable for large state spaces
5. Useful for approximate solutions

Disadvantages of Hill Climbing

1. Not guaranteed to find global optimum
2. Gets stuck in local maxima
3. Incomplete algorithm
4. Cannot backtrack
5. Sensitive to starting point

Applications of Hill Climbing

• Scheduling problems
• Game playing AI
• Robot navigation
• Feature selection
• Resource allocation
• Optimization problems
• Machine learning optimization (basic level)

Time and Space Complexity

• Time Complexity: Depends on number of iterations and neighbors
• Space Complexity: $O(1)$O(1) (only current state stored)

Hill Climbing in Artificial Intelligence

Hill climbing is widely used in AI where:

• Exact solution is not required
• Approximate solution is acceptable
• Search space is very large

Many advanced algorithms are extensions of hill climbing, such as:

• Random restart hill climbing
• Simulated annealing
• Genetic algorithms (conceptually related)

Conclusion

Hill Climbing is a heuristic-based local search algorithm that incrementally improves a solution by moving toward better neighboring states. It is memory efficient and fast but suffers from problems such as local maxima, plateaus, and ridges. Due to these limitations, hill climbing is neither complete nor optimal, yet it forms the foundation of many advanced optimization techniques in artificial intelligence.