DEPTH FIRST SEARCH (DFS)

Introduction

Depth First Search (DFS) is one of the most important and fundamental graph traversal algorithms used in Computer Science, Data Structures, and Artificial Intelligence.
Traversal means visiting all the nodes of a graph in a systematic manner.

DFS explores a graph by going as deep as possible along a path before coming back and trying other paths. Because of this nature, DFS is closely related to backtracking.

Definition

Depth First Search (DFS) is a graph traversal algorithm in which exploration starts from a given source node and proceeds as deep as possible along one branch before backtracking.
It follows the principle “Go deep first, then come back”.

DFS can be applied to graphs as well as trees and is widely used in Artificial Intelligence search problems, path finding, cycle detection, and backtracking-based problems.

In simple words:

DFS goes deep first, not wide.

Basic Idea of DFS

• Start from a source node
• Visit the node and mark it as visited
• Move to one of its unvisited adjacent nodes
• Continue moving deeper until:
  • no unvisited adjacent node is left
• Then backtrack to the previous node and explore other paths

This behavior is similar to exploring a maze by choosing one path and continuing until you hit a dead end.

Data Structure Used

DFS uses:

• Stack
  • Either an explicit stack
  • Or implicit stack using recursion

This is why DFS follows LIFO (Last In First Out) order.

Step-by-Step Working of DFS

1. Choose a starting (source) node
2. Mark the source node as visited
3. Visit one of its unvisited adjacent nodes
4. Repeat the process for that node
5. Continue until:
6. No unvisited adjacent node is left
7. Backtrack to the previous node
8. Explore remaining unvisited neighbors
9. Stop when all nodes are visited

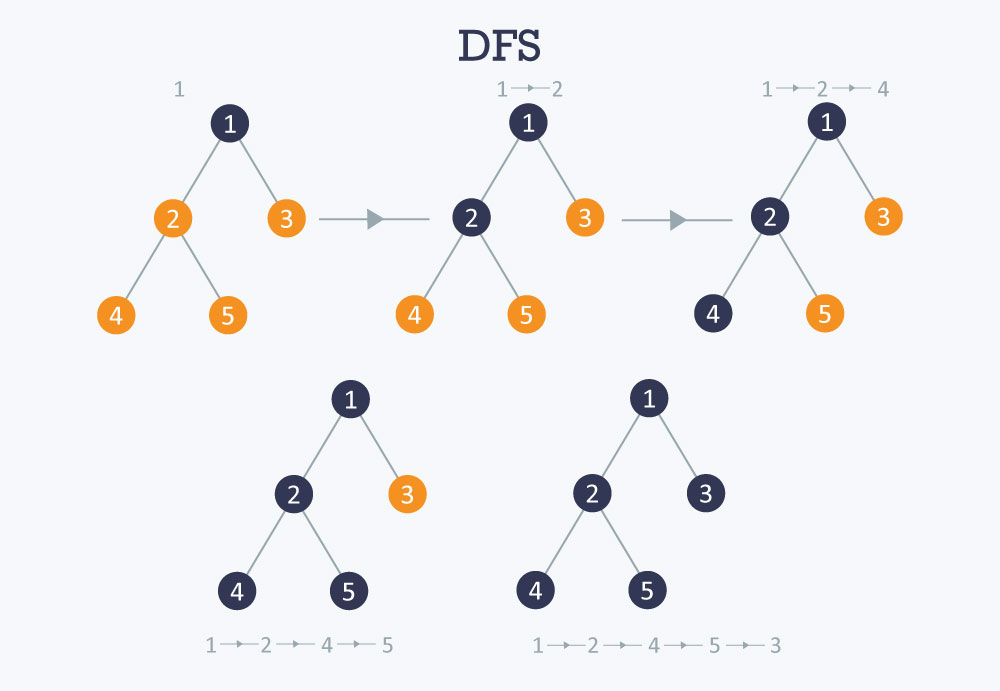
Example of DFS Traversal

Consider the following graph:

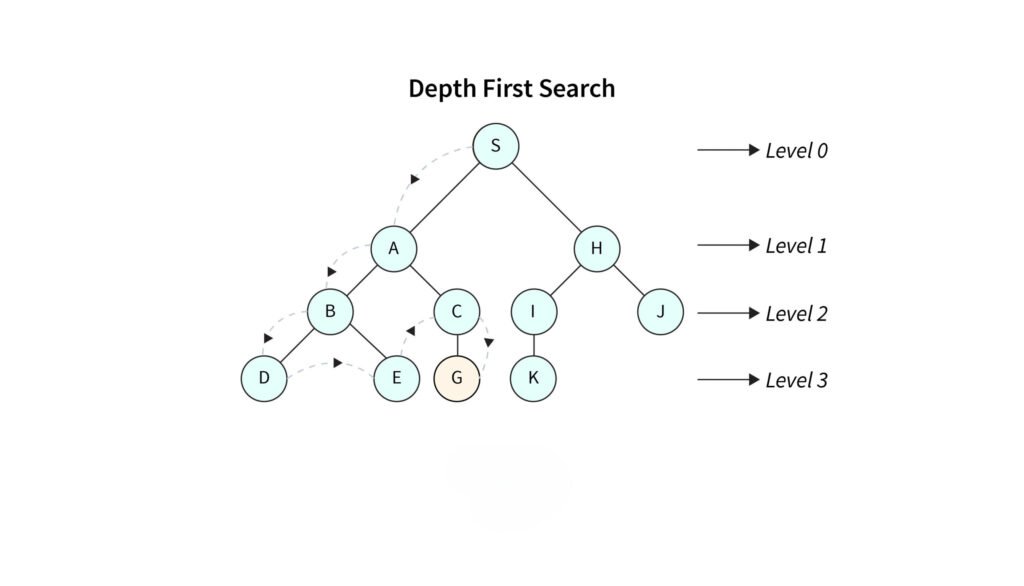
NOTE : Upper image is different from the example.

FOR EXAMPLE :

Graph Structure

• Nodes: A, B, C, D, E, F
• Edges connect nodes in multiple paths

DFS Traversal Starting from Node A

1. Start at A
2. Move to B
3. Move to D
4. No further unvisited nodes → backtrack to B
5. Move to E
6. Backtrack to A
7. Move to C
8. Move to F

A → B → D → E → C → F

DFS Algorithm (Conceptual Explanation)

• DFS begins with the root node
• It marks nodes as visited to avoid repetition
• The algorithm keeps moving deeper until it reaches a dead end
• When a dead end is reached, DFS backtracks
• This process continues until all nodes are explored

Why DFS Uses Backtracking

Backtracking allows DFS to:

• Return to previous nodes
• Explore alternate paths
• Ensure complete traversal

This makes DFS very useful in:

• Puzzle solving
• Decision trees
• Constraint satisfaction problems

Applications of DFS

DFS is widely used in:

• Maze solving problems
• Path existence checking
• Cycle detection in graphs
• Topological sorting
• Finding connected components
• Artificial Intelligence search problems
• Solving puzzles like Sudoku, N-Queens

Advantages of DFS

1. Requires less memory compared to BFS
2. Easy to implement using recursion
3. Suitable for problems where:
   • Solutions are deep
4. Efficient for sparse graphs

Disadvantages of DFS

1. Does not guarantee shortest path
2. May get stuck in infinite depth
3. Not suitable for:
   • Very deep or infinite graphs without limits
4. May explore unnecessary long paths

Time and Space Complexity

• Time Complexity:
  $O(V + E)$O(V+E)
  where:
  • V = number of vertices
  • E = number of edges
• Space Complexity:
  $O(V)$O(V) due to recursion stack

Conclusion

Depth First Search is a fundamental graph traversal algorithm that explores nodes by going deep into a path before backtracking. It is memory efficient and easy to implement, making it suitable for backtracking and deep search problems. However, it does not guarantee optimal solutions and may fail in infinite or very deep search spaces. Despite its limitations, DFS forms the foundation for many advanced algorithms in computer science and artificial intelligence.

ALSO READ – BREADTH FIRST SEARCH (BFS)